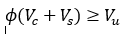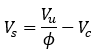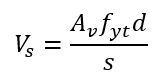One-Way Shear
Code References
ACI 318-14
ACI 318-19
Definition
For the purposes of this discussion, one-way (or vertical) shear is defined as the shear force perpendicular to the axis or span of the member. Also, the discussion in this section is limited to precast concrete members that span horizontally and are governed by the ACI 318 Specification. Note, one-way shear is how it is defined in the ACI 318 code, it is also known as beam action shear.
Basic Equation
The shear resistance of precast concrete components must meet the following requirement (22.5):
where:
Vc = nominal shear strength provided by concrete
Vs = nominal shear strength provided by shear reinforcement
φ = reduction factor as defined in the governing specification
Critical Sections
For simply supported horizontal members, 9.4.3.2 has defined the critical section for shear to be a distance d from the face of the support for non-prestressed members and h/2 for prestressed members. If a concentrated load is present between the critical section and the face of the support, then the face of support should become the critical section. For members that do not have the loads applied at the top of the section or are non-simply supported, then the critical section should conservatively be located at the face of the support.
If the non-composite section is being used for shear resistance, then the non-composite height is used to calculate d and H. If the composite section is being used for shear resistance, then the composite height is use. The user must also make an affirmative response to move the critical section away from the support face.
Member Orientation
When computing shear capacity, it is computed in line with the appeared shear vector. If flexure is computed about a different angle, the 'd' value is computed for the orientation corresponding with the shear force. ACI 318-14 gives no guidance on the direction you should compute it in. ACI 318-19 allows the computation of it about any axis with equations for the interaction. By aligning our orientation with the applied load, we bypass the need to perform any shear interaction.
Calculation of Vc
All values of f’c used in determining Vc are reduced by the appropriate factor if using lightweight concrete. Note that the analysis uses the base area of prestressing strand, ignoring development length, to determine if a member is prestressed or non-prestressed.
For composite members, the shear area (and the depth thereof), is dependent on whether the composite topping is to be considered a part of the shear resisting section. The final strength of the precast section at all times to calculate the shear resistance, even when the user selects the use of the composite section. The full depth is also used in the calculation of d (with a lower limit of 0.8*H), except where d is used in the term V*d/M, then the actual d is used with the limit of 0.8*H.
For all beams (both prestressed and non-prestressed), the minimum shear strength is 2 * √(F’c).
Shear Area
The shear area is calculated based on the polygons which make up the cross section, which are used in place of the bd term in the equations for Vc. Some sections (typically the sections which consist of webs and top/bottom flanges), only the polygon which encompasses the web is used (and extending this polygon into the top and bottom flanges, if present). This polygon is extended into the topping if the composite shear resistance section option is selected by the user.
Based on the figure below, the shear area (shown in red) is computed based on the concrete used in shear above d. This means sections with drafts are more accurately handled when computing shear.
Mild Reinforced (non-prestressed) Members
ACI 318-14
For non-prestressed members, the analysis uses the appropriate equation based on the sign of the of the axial load (compression – 22.5.6, tension – 22.5.7, or none – 22.5.5). Note that both the ‘tension’ and the ‘compression’ equations become the ‘no axial load’ equation when the axial load is equal to zero. For both no axial force and axial compression, both the detailed and the simplified methods are used, and the program selects the greater of the two values (the axial tension section does not include a detailed method for the calculation of Vc).
Beams without any mild reinforcement in tension (that is an undefined d value) will use 0.8h in place of d. This is not supported by the code and typically only happens at the ends of the beam, where shear is not typically checked.
ACI 318-19
For non-prestressed members, the analysis follows section 22.5.5. When following this section, the program behaves in two different methods depending on if the program is computing Av required or if the user entered transverse reinforcement.
Computing Av Required
When the software is computing Av required, we first assume the user is not providing minimum shear reinforcement. Because Av min is not met, we use equation 22.5.5.1c. Once Vc is computed, we see if the user must provide minimum shear reinforcement per chapter 7 or 9 (depending on the member). If minimum shear reinforcement is required, Vc is then recomputed using the minimum of equations 22.5.5.1a and 22.5.5.1b.
Computing ϕVn
When the user inputs their transverse reinforcement, the program computes ϕVn instead of computing Av Required. For these cases, it is just checked if Av provided exceeds Av Min before determining which equations of Table 22.5.5.1 to use.
Prestressed Members
For horizontal prestressed members, the analysis uses the traditional Vci/Vcw equations to determine the shear capacity of the concrete (22.5.8.3). The approximate method for calculating Vc as shown in the equations tabulated in the ACI 318 code (Table 22.5.8.2) is typically reserved for members that span vertically and are therefore unavailable for horizontal members in this analysis. The nominal concrete shear strength determined using this approach includes the upper and lower limits as noted in ACI 318.
Minimum Shear Strength
The concrete shear strength is also assumed to have a minimum strength equal to the plain concrete shear strength as defined in Table 14.5.5.1.
Calculation of Vs
When no transverse reinforcement has been defined, the amount of shear required to be resisted by shear reinforcement, Vs, is calculated by:
The strength of the provided transverse reinforcement, when applicable, is computed by summing all of the zones the location overlaps with. Eriksson Beam computes the total transverse provided based on the transverse inputs and used in Eq. 22.5.10.5.3.
Required Shear Reinforcement
For one-way slabs, 7.6.3.1 requires a minimum area of shear reinforcement where Vu > φVc unless tests have proved that the components develop the required strength without reinforcement. For most beams (9.6.3.1), minimum shear reinforcement is required where Vu > 0.5φVc. See notes at the end of this discussion for Av,min requirements of specific section types. Note that there are different equations for Av,min for non-prestressed and prestressed members, but the same equation for Av is used for both types of members (inclined stirrups may be used for non-prestressed members).
Note that there are two Vs terms used in the program, one is Vs,reqd, based on Vu-Vc, and the second is Vs,prov, based on the area of shear steel input by the user.
When the critical section is not located at the face of support, Av,reqd is still calculated between the face of support and the critical section.
The program also calculates a maximum value of φVn (22.5.1.2), which is essentially an upper limit on Vs.
One way shear capacity is calculated at every analysis point in the member. At each point Eriksson Beam computes either the required area of steel, or checks the provided area of steel against the calculated amount. When comparing a provided amount against required, this is assuming all steel being provided is to be used for shear and is taking torsion into account. The combined effects are taken into account in the combined shear and torsion section.
For all sections, including double T’s and risers, the reported required area of steel is for the entire member and not per stem or bearing point.
Maximum Spacing Requirements
The maximum spacing required for shear reinforcement based on 9.7.6.2.2 is calculated and displayed for the user. Vertical stirrups comprised of mild rebar is typically used for shear reinforcement. Welded wire reinforcement may also be used. Anchorage requirements for shear reinforcement can be found in 25.7.1.4 and 25.7.1.5.
Cross Section Limits
The cross section limits are checking against ACI 318-14 22.5.1.2. If the limits fail and error will be displayed in the analysis report.
Hand Calculation
Exceptions and Notes
In the case of single and double tees, when they are simply supported, uniformly loaded, and when they require little or no shear reinforcing as calculated for Avcw, and approximately 0.04 in2/ft or less of shear reinforcing as calculated for Avci, the engineer may omit the leg mesh in the middle 80% (+/-) of the span.
For the case of hollow core slabs, if the untopped section depth is <= 12.5 in., then no minimum shear steel is required. If the untopped depth is > 12.5 in., then minimum shear reinforcement is not required where Vu <= 0.5φVcw. Currently, the analysis does not take this provision into account.
Note that required shear reinforcement does not include any suspension steel that may be required for ledges. A separate ledge analysis is required.
Critical section for shear. The critical section for shear is based on the depth of the resisting element, and assumes that the loads on the beam (including self-weight) between the critical section and the support go directly into the support without the mechanism of beam action (acting kind of like a small column). The depth used to calculate the critical section should be based on the cross section used to resist shear. If there is an applied concentrated load between the critical section and the support, then the critical section is the face of the support.
References
ACI Committee 318, Building Code Requirements for Structural Concrete (ACI 318-14), American Concrete Institute, Detroit, 2014.
Aswad, Burnley, Cleland, Orndorff, and Wynings, “Load Testing of Prestressed Concrete Double Tees Without Web Reinforcement,” PCI Journal, V. 49, No. 2, March-April 2004, pp. 66-77.
PCI Industry Handbook Committee, PCI Design Handbook, 8th Ed., PCI, Chicago, 2017.