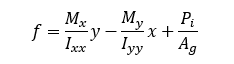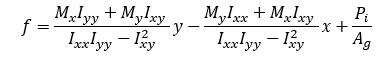Stress Calculation
When calculating stresses for a given longitudinal location, each vertex in the cross-section’s polygon is checked. This guarantees that the controlling stresses are found and accounts for all asymmetries in the cross-section, the prestressing force, and any lateral loading that may exist. If the cross-section is composite the stresses are split into the stresses on the non-composite cross-section and the stresses on the composite cross-section. These stresses are calculated individually, and the total stress is the sum of the two values. Non composite stresses include forces from self-weight, non-composite dead load, topping weight, and the prestressing force. Composite stresses come from all other load types.
Symmetric Sections
For symmetric sections, the stress at a given location is as follows:
Where:
Mx is the moment about the horizontal axis,
My is the moment about the lateral axis,
Pi is the axial force,
Ixx is the moment of inertia about the x axis,
Iyy is the moment of inertia about the y axis,
and Ag is the area of the concrete.
Prestress Force
The prestressing force generates both axial force and internal moments on the member. The prestressing moments generated can be about either the horizontal axis or the vertical axis depending on magnitude and location of the strand eccentricities. Lateral strand eccentricity, which generates moments about the vertical axis, can often be ignored, especially in members such as L-Beams or asymmetric Double Ts. However, spandrels cast on their side can generate significant stresses about the vertical axis.
Principal Stresses
Stresses due to asymmetric sections are accounted for by modifying the stress equation above. The general form of the stress equation above is as follows:
Where:
Ixy is the product of inertia.
Note that in the equation for asymmetric cross-sections, if the product of inertia is zero the equation simplifies to the same equation used for symmetric cross-sections.