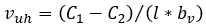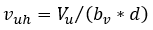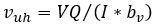Horizontal Shear
General Discussion
A composite member is defined herein as the use of a CIP (cast-in-place) concrete slab placed upon and interconnected to a precast beam so that the combined beam and slab will act together as a unit. Horizontal shear stresses act on the interface in a composite member, and as a result, the slab and beam act in a composite manner. Horizontal shear stresses are resisted using both horizontal shear transfer and shear friction. Although the mechanism of horizontal shear transfer and that of shear friction are similar if not identical, there is a considerable difference between the two sets of provisions in the ACI 318 code.
Design Procedure
The design procedure is straight forward. 1) Calculate the demand (vuh) using one of three methods presented here. 2) Calculate the capacity of the concrete interface. 3) Calculate any required Avh using equations from ACI 318, assuming either a roughened interface or a smooth interface.
Methods of Calculating Demand
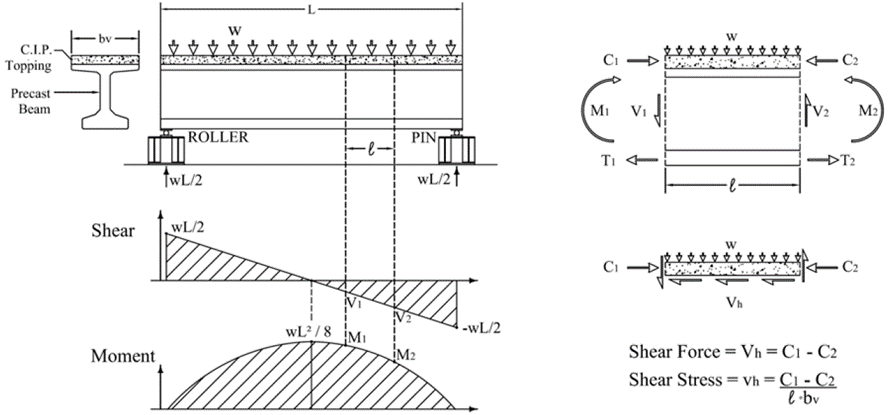
Global Force Equilibrium method
The global force equilibrium method obtains the horizontal shear stress from the change in compression forces occurring in the topping slab between two points along the beam, and can be shown in the following figure:
From this method, the horizontal shear stress can be calculated as
This is the method found in the PCI Design Handbook in Section 5.3.5. For simplicity (and good practice), it is generally assumed that C2 is equal to zero.
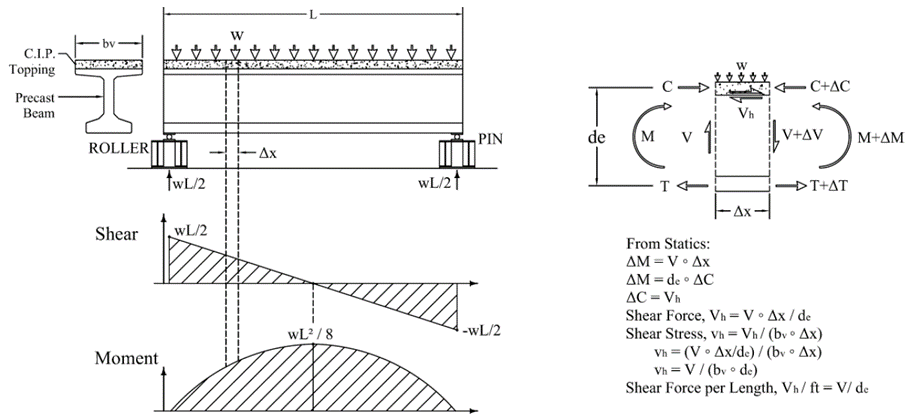
Simplified Elastic Beam Behavior method
Simplified elastic beam behavior uses flexural beam theory to equate the horizontal shear stress equal to the vertical shear acting on the section. This can be shown in the following figure:
From this method, the horizontal shear stress can be calculated as
Classical Elastic method
The classical elastic method has been used for years to calculate the horizontal shear stress of beams. This method is based on the elastic response of a beam, and therefore may not be valid if the section is cracked.
Using this method, the horizontal shear stress is calculated as
Note that the uncracked transformed section properties are generally used to calculate the elements of this equation.
Capacity Calculations (from ACI 318 16.4)
The capacity of the horizonal shear plane is the same regardless of the method of calculating demand and is taken from ACI 318. The procedure can be broken down between roughened and smooth interfaces, both of which can be further divided into sub-steps.
For Roughened Concrete Interfaces
If vuh < φ*80 psi, no ties required
If vuh > φ*80 psi, at least minimum ties required
If vuh > φ*260 psi (roughly), more than minimum ties are required
If vuh > φ*500 psi, capacity must be determined using shear friction
Note that the shear friction methodology can be used at any level of vuh. If vuh is less than φ*500psi, then you can use the lesser of the Avh calculated from shear friction and that calculated from assuming either minimum Avh or some amount of reinforcement greater than minimum. The effective μ from PCI can be used in the shear friction equation.
For Smooth Concrete Interfaces
At any level of vuh, you should set Avh equal to the larger of minimum ties or that determined using shear friction requirements. Use a value of 0.6 for μ in the shear friction equation, and in this case, you are not allowed to use effective μ.
The value of d used in the ACI equations is dependent on method of calculating vuh. Use lvh (=l/2) when using the PCI method (Global Force Equilibrium). Use the distance from the compression fiber to the centroid of the reinforcement when using other two methods.
Miscellaneous Notes
For the calculation of the maximum allowable Vnh, use the smaller of the two concrete strengths (precast/CIP).
For the calculation of Av,min, use the larger of the two concrete strengths (precast/CIP), and use bw (width of the section used to resist vertical shear), not bv (width of the horizontal shear interface).
When using the VQ/Ib approach, the method of transforming steel matters.
References
ACI Committee 318, Building Code Requirements for Structural Concrete (ACI 318-14) and Commentary (318R-14), American Concrete Institute, Detroit, 2014.
ACI Committee 318, Building Code Requirements for Structural Concrete (ACI 318-19) and Commentary (318R-19), American Concrete Institute, Detroit, 2019.
Kovach, J., Naito, C., Horizontal Shear Capacity of Composite Concrete Beams without Interface Ties, ATLSS Report No. 08-05, Bethlehem, June 2008.
PCI Industry Handbook Committee, PCI Design Handbook, 8th Ed., PCI, Chicago, 2017.